PAPELES EN TENSION

INTROITO

Estimados lectores: Agradezco profundamente todos los comentarios que realizaron con respecto a la entrada anterior. A los que van a leer este blog por primera vez les recomiendo empezar con la entrada anterior: UN PASATIEMPO DE DECISIONES. Como se habrán dado cuenta, le he cambiado el nombre al blog por EL CODIGO D'CP, esto con el fin de hacerlo más atractivo e interesante. Además le he creado un logotipo, el cual pueden ver a su derecha. El logotipo tiene un acertijo en si mismo. Agradecería me escribieran cuando lo entiendan. Por último, por supuesto que yo también desearía que las entradas fueran más seguidas pero mientras no domine todos los recursos para ilustrar adecuadamente mis ideas, debo mantenerme con entregas cada quince días. Las ideas se me agolpan en la mente y desean salir ya, para que ustedes las analicen pero hay que contenerlas y organizarlas para después entregarlas. Por ahora están en mi cuaderno físico pero ya las mostraré en mi cuaderno virtual. Algún día talvez realice entregas semanales. ¡Ya veremos! También estoy trabajando para llegar a las personas de habla inglesa.

Atentamente,

Ing. Eric Madrigal
Asociación Costarricense de Origami

Nota: algunas palabras o frases aparecerán en verde.
Esto significa que son añadidos ulteriores a la publicación
de la entrada y por sugerencia directa de los lectores.


I PARTE:

LA ECUACION:

El Tangram, ¿quién no conoce este milenario pasatiempo chino? Tomamos un cuadrado y lo dividimos en siete figuras geométricas básicas: 5 triángulos rectángulos isósceles, 1 cuadrado y 1 paralelogramo. Un instructivo con las siluetas de miles o tal vez millones de figuras nos invita a colocar esas 7 figuras geométricas en arreglos planos y obtener las siluetas. Entonces en el Tangram dividimos un cuadrado, obtenemos unas figuras geométricas y construimos siluetas:

¿Que tiene que ver esto con los CPs? Pues bastante!. En el capítulo ocho del libro Origami Design Secrets, el Dr. Robert Lang, hace un excelente estudio de lo que se denomina en origami "Tiling". Lang señala que un CP está compuesto de figuras geométricas que se ensamblan en un cuadrado, siguiendo ciertas normas básicas, tal como si fuese un mosaico. Por lo tanto, a partir de un modelo de origami se obtienen, al desdoblar, las marcas del CP; y sus intersecciones conforman figuras geométricas. Lo interesante es que todas quedan ensambladas perfectamente en un cuadrado. Por lo tanto tenemos:

Ahora me entienden el porque uso esta metáfora: que el CP es el inverso del Tangram. Claro que el Sr. Lang en su libro está hablando sobre diseño de nuevas bases para modelos de origami, pero creo que podemos generalizar. Ya sea que el modelo esté en la mente de creador o que ya esté doblado y se desdoble, la verdad es una: un CP está compuesto de múltiples figuras geométricas inmersas en un cuadrado. Por lo tanto, en el proceso de resolución de CPs una de las primeras acciones que debemos realizar es:

PRIMERA PISTA

RECONOCER LAS FIGURAS GEOMETRICAS

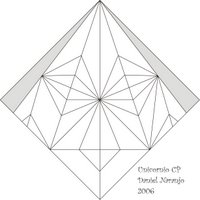
Para ilustrar lo anterior, recurriremos a un CP del origamista colombiano Daniel Naranjo y a las imágenes de los Tipos de Triángulos en el capítulo anterior. (Si tocamos el CP veremos el modelo final del autor)

Fig.1: CP de Daniel Naranjo

La pregunta sería : ¿cuántos triángulos y de qué tipos aparecen en el CP de Daniel? ¿Qué otras figuras geométricas podemos reconocer en él y cuantas de cada una?

Aunque a primera vista parece fácil resolver estas preguntas, les diré que no lo es. Para resolverlas tenemos que utilizar algún método. El que yo les recomiendo es un proceso de discriminación visual. Además este método me permitirá indicarles algunas conceptos básicos más en la resolución de CPs.

II PARTE:

CONTANDO FIGURAS GEOMETRICAS

Cuando observamos un CP, especialmente los más complejos, se nos presentan muchas hermosas combinaciones de figuras geométricas y si quisiéramos reconocerlas y contarlas de seguro nos sentiríamos pronto un poco confundidos. Es por ello que la primera pista nos invita a reconocer las figuras geométricas en el CP. Vamos a dar la segunda pista:

SEGUNDA PISTA

SELECCIONAR LAS FIGURAS GEOMETRICAS INCLUIDAS

ENTRE LAS LINEAS MÁS LARGAS DEL CP

Bien!, podemos ver en el CP de Daniel que las líneas más largas cortan el CP en 4 figuras geométricas básicas. Las demás líneas, normalmente más cortas, las dejaremos para después.

Si queremos contar triángulos pues ya tenemos cuatro. Este es el conteo al "Primer Nivel" que es el más importante.

El siguiente paso nos lleva a la tercera pista:

TERCERA PISTA

ENCONTRAR LAS LINEAS DE SIMETRIA DEL CP

Es muy común que un CP sea simétrico con respecto a una o varias líneas; o sea, que todo lo de un lado de la línea se repite en el otro (sobre simetrías ya analizaremos bastante en su debido momento). Por lo tanto, para contar los triángulos, podemos desentendernos de las otros mitades del CP, contar y luego multiplicar por dos. De este modo reducimos bastante el trabajo.

Al cortar en la línea de simetría se nos generan dos nuevos triángulos y multiplicando por dos tenemos cuatro triángulos. ¿Como va el conteo de triángulos? Pues, llevamos ocho. Este es el "Segundo Nivel". Veamos ambos niveles:

Fig.2: Divisiones al primer y segundo nivel

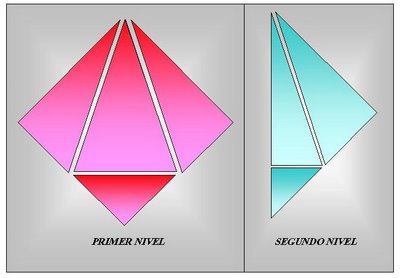
Los niveles pueden proseguir realizándose de acuerdo a conveniencias y dependen también fuertemente del CP que estemos analizando. En este blog voy a indicar solo dos niveles más y que sirvan de ilustración. Para el "Tercer Nivel" cortamos todos las figuras geométricas dentro de uno de las áreas del segundo nivel.

Tenemos ahora 20 nuevos triángulos y por 2 son cuarenta triángulos más. Total 48 triángulos.

Al cuarto nivel vamos a agrupar los triángulos, de dos en dos, luego de tres en tres, y así hasta el final. Solamente les muestro la agrupación en dos y tres de uno de los triángulos principales. Veamos los niveles 3 y 4:

Fig. 3: Divisiones al tercer y cuarto nivel

Bueno ya me canse!. Por dicha solo los primeros niveles son normalmente los importantes. A continuación les muestro una tabla con el total de todos los triángulos que encontré entre las líneas del CP de Daniel; pero les notifico que hay también, rombos, cuadrados, pentágonos, trapecios, etc que ustedes con paciencia pueden descubrir.

TABLA DE CONTEO DE TRIANGULOS

Para finalizar esta parte me gustaría mostrarles el TANGRAM INVERSO de Daniel Naranjo:

Fig. 4: CPD del Unicornio de Daniel Naranjo

!Hermoso!, ¿verdad?...

Dado que en algunos momentos utilizaremos, en este blog, este recurso para estudiar los CPs me gustaría llamar a este tipo como CPD o sea CP dividido y entendemos, dividido en sus figuras geométricas fundamentales. Dado que habrá muchas formas de dividir el CP, la división será seleccionada únicamente por concepto de conveniencia.


III PARTE

LA SERIE EQUIS

En la última entrada nos terminamos preguntando que sucederá cuando a nuestros CPs más sencillos les incorporemos una nueva línea. Lo que sucede, al fin y al cabo, es que la Primera Incertidumbre Espacial se vuelve de vital importancia. Ya veremos el porqué.

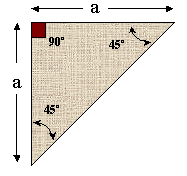
Tomemos nuestro CP de la Bisectriz y tracemos la otra Bisectriz. Con ello dividimos las cuatro esquinas del papel en ángulos de 45º cada uno; además nos aparece una intersección de ambas líneas y se forman cuatro triángulos isósceles rectos, cada uno de un cuarto del área del cuadrado original. Veamos el CP:

Fig. 5: CP Bisectrices______Fig. 6: Vértices y rayos

Este CP con forma de equis nos permite introducir dos nuevos conceptos muy importantes. El punto 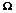, la letra griega omega, en la figura 2, que corresponde a la intersección de las dos diagonales y que se ubica exactamente en el centro del papel, es un ejemplo de un VERTICE o NODO. Los vértices son puntos en el plano donde se cruzan varias líneas. Si retomamos nuestra metáfora del embrión, el punto sería el ombligo del embrión, y será un punto muy importante para este blog.

Otra forma en que se puede considerar el vértice y que personalmente preferiré en este blog, es considerarlo como un punto del cual irradian varios segmentos de línea. Estos segmentos de línea son conocidos como RAYOS. En la figura 6 hemos marcado con rojo uno de estos segmentos. Por lo tanto, el vértice mostrado divide cada diagonal en dos partes exactamente iguales generando cuatro rayos que irradian de él.

Vamos a jugar un poco con estos rayos y ya verán que cosas interesantes van a suceder. Tomemos un papel y procedamos a doblar el primer CPMV con todos los rayos en valle, tal como se muestra en la siguiente figura.

Fig. 7: CPMV con solo valles

Marquemos muy bien el valle por cada rayo. ¿Qué observamos? Correcto. El papel queda en tensión y se provoca una curvatura en cada superficie de los cuatro triángulos isósceles rectos. La orilla del papel también esta curva. Aprovecharé esta curvatura del papel para realizar varias figuras tridimensionales de origami, las cuales llamaré LA SERIE X.

Con el CPMV todos en valle les muestro las siguientes imágenes: La Madonna y La lágrima.

_

Fig. 8: LA MADONNA________Fig.9: LA LAGRIMA

El CP corresponde , por supuesto, a la base de la figura. Por lo tanto, no se muestran los dobleces para hacer el bloqueo final de la figura. Pero la verdad, es muy fácil!

En el siguiente CPMV los rayos se alteran entre valles y montañas. Veámoslo y procedamos a doblarlo (observar que el resultado es una diagonal en valle y la otra en montaña). Una figura más se puede generar en la Serie X: El Beso.

Fig. 10: CPMV mixto

Fig. 11: EL BESO

Por último, el siguiente CPMV muestra dos rayos adyacentes en valle y los otros dos en montaña. Como resultado les muestro dos figuras más de la Serie X: El Angel y El Benedictino.

Fig. 12: CPMV mixto

Fig. 13: EL ANGEL

Fig. 14. EL BENEDICTINO

Resumiendo, de un mismo CP hemos obtenido tres CPMV y seis figuras simples y elegantes de origami.

Entendemos ahora el problema de la PRIMERA INCERTIDUMBRE ESPACIAL. Al asignarle valles y montañas a las líneas de los CP se pueden generar varias combinaciones y los resultados son diferentes debido a las relaciones entre ellas. En CPs muy complejos tenemos múltiples vértices y muchísimos rayos y se deben tomar decisiones a cada momento sobre cuales son valles y cuales montañas. Por dicha, el origami vendrá en nuestro auxilio para darnos algunas luces sobre como proceder. ¡Ya lo verán!

Un procedimiento similar podemos realizar con las mediatrices. El CP de las dos mediatrices se muestra en la siguiente figura:

Fig. 15: CP Mediatrices

El vértice de las dos mediatrices cae también exactamente en el centro del papel y los rayos dividen el mismo en cuatro cuadrados cada uno un cuarto del área del cuadrado original. Para este CP solo mostraré un CPMV con todos los rayos en valle y una sola figura: el Murciélago.

Fig. 16: CPMV

Fig. 17 : EL MURCIELAGO

Todas las figuras obtenidas son evidentemente tridimensionales y no se pueden aplanar sin introducir nuevos dobleces. Vi un video en que el genial origamista Robert Lang marca las dos diagonales o las dos mediatrices y siguiendo las curvaturas del papel logra marcar los siguientes dobleces que forman las figuras planas multicapas. El papel parece suplicar con su curvatura la introducción de esos dobleces para así eliminar la tensión y entrar en sosiego. Esta súplica es realmente una variable física: la tensión mecánica. La tensión mecánica se define como el valor de la distribución de fuerzas por unidad de área en un cuerpo sólido. Es como cuando se jala una cuerda por ambos extremos. Como bien sabemos, el papel está compuesto por fibras vegetales y adhesivos que las compactan. Al marcar líneas sobre el papel las fibras se tensan y generan estas curvaturas. Veámoslo en la siguiente imagen para que me entiendan:

Fig. 18: Papel en tensión

Muchos CP que observamos tienen entre sus líneas el embrión de figuras planas multicapas y otros el de figuras tridimensionales. En algún momento de nuestro aprendizaje estudiaremos juntos el requisito para que una figura sea plana multicapa. Pero eso será más adelante.

Por ahora nos falta todavía bastante camino por avanzar y muchos conceptos básicos por dominar. Para aprender más aún utilizaremos las BASES TRADICIONALES del origami japonés, pero esto será en nuestra próxima entrega.

En este blog tus comentarios son extremadamente importantes; por favor escribirlos abajo. Si no tienes una cuenta ni un password no se preocupe, toque donde dice anónimo y allí puede escribir su mensaje.
Si deseas una copia en formato pdf de este documento solicítamelo a la dirección eric@internetelfaro.com que con mucho gusto te lo enviaré.

Hasta dentro de 15 días....

UN PASATIEMPO DE DECISIONES

INTROITO

Estimados lectores: cumpliendo con mi compromiso de entregas cada 15 días, aquí coloco a su consideración la segunda entrada de mi blog. Les recuerdo que son mis notas de como voy aprendiendo todo lo relacionado con resolución de CPs. Pido disculpas por los errores que cometo, especialmente relacionados con los dibujos, el manejo del lenguaje html y de las imágenes que aún estoy en proceso de dominar. ¡Cada día aprendo más!

Atentamente,

Eric Madrigal
ACRO

Nota: algunas palabras o frases aparecerán en verde.
Esto significa que son añadidos ulteriores a la publicación
de la entrada y por sugerencia directa de los lectores.

1. PRIMERA PARTE:

LOS MISTERIOS DE ROMAN

Hace 15 días les mostré dos hermosos CPs del origamista Román Díaz y les indiqué, además, que entre sus líneas estaban ocultos grandes misterios. Para comenzar a entender los CPs me gustaría mostrarles uno de esos grandes misterios. Para ello, favor tocar la imagen que dice BASE.

___

CP__________________BASE

¡Eso es! Uno de los grandes misterios ocultos entre las líneas de los CPs es el modelo final del creador (en la entrada anterior, Introducción y Definición de CP, si tocan el otro CP se les revelará el otro modelo de Román).

A decir verdad, el modelo final está allí como una mariposa en el capullo. Y, ¿por qué lo expreso de esta manera? Porque es de gran importancia que entendamos muy bien los CPs y de este modo establezcamos los debidos límites de nuestro pasatiempo.

El CP usualmente nos lleva solo hasta lo que se denomina la BASE. En la terminología del Origami, la BASE de un modelo es una etapa en la secuencia de doblado en la que se obtiene una figura con la misma cantidad, distribución y tamaño de puntas o aletas principales que el modelo final. Algunas veces esa figura se parecerá al modelo final, pero por lo general no. Por lo tanto, para adentrarnos en este maravilloso pasatiempo que es la resolución de CPs, debemos quitarnos primero el deseo de obtener con ellos el modelo final del creador. Por supuesto, que a título personal y dependiendo de las capacidades de cada persona, muchos lograrán, mediante técnicas de origami, llegar al modelo final; pero eso ya estará fuera de los alcances de este blog.

En casos muy particulares, se logra encontrar creadores de origami bastante benévolos en cuyos CPs casi que se obtiene el modelo final, pero eso no es lo más común. Por lo tanto, como señalamos anteriormente lo más usual es que el CP nos lleve hasta la base, o hasta algún punto entre la base y el modelo final; pero definitivamente muy pocas veces hasta el modelo final y definitivamente nunca hasta antes de la base.

¡Me gusta pensar en la base!. La considero como un embrión del modelo final. En el CP-embrión está todo lo necesario o estructuralmente importante (ver definición de CP en la Introducción) para obtener la figura final, ¡pero le falta siempre algo más! Le falta crecer, desarrollarse, definirse y formar los detalles, para, de esta forma, al final, nacer. Los CPs son hermosos, con sus simetrías, sus vértices, de los cuales irradian múltiples rayos, formando como estrellas y el modelo final es grandioso, con su prestancia y representatividad; pero la base, a mi parecer es fea igual que un embrión. Muchas personas viendo el CP se sienten atraídas por resolverlo y al ver el modelo final desean obtenerlo, pero solo muy pocas, relativamente, sabiendo la verdad, persisten en desgastar su mente por el puro amor al "feo" embrión.

2. SEGUNDA PARTE:

LOS CPS MAS SENCILLOS Y SUS INCERTIDUMBRES

Las dos figuras de origami, con los CPs más sencillos que existen, sirven para representar montañas, volcanes, techos, libros, puertas, y miles de cosas más. Son de una gran antigüedad y sus orígenes se pierden en la nubosidad de la historia no documentada. Mostrarlos podría parecer trivial pero, como bien nos enseña el método inductivo, las cosas simples nos ayudarán a entender las complejas. En estos dos CPs están contenidos varios conceptos fundamentales que serán ampliamente utilizados en la resolución de CPs cada vez más complejos. Veamos los CPs trazados en un papel cuadrado:

(Fig.1) CP1: Bisectriz______ (Fig.2) CP2: Mediatriz

La línea del CP1 se denomina Bisectriz o Diagonal y corta el ángulo recto, de dos esquinas opuestas, exactamente en ángulos de 45°. Las figuras a ambos lados de la bisectriz son dos triángulos rectángulos isósceles, cada uno de ellos con un área que es la mitad del área del cuadrado original (¡Ojo los profesores de primaria, esto puede servir como método visual para la enseñanza de la geometría! Este blog contendrá muchos elementos que les pueden ser de utilidad.). Veámoslo con más detalle para que quede bien claro:

(Fig. 3) Cuadrado dividido__________(Fig.4) El triángulo separado

El triángulo es rectángulo por contener un ángulo de 90º y es isósceles puesto que tiene dos lados iguales.

El reconocimiento de figuras geométricas básicas y los conceptos matemáticos que las gobiernan será una parte fundamental en el proceso de resolución de CPS. Iremos poco a poco reconociéndolas una a una.

Por ahora solamente me gustaría mostrarles, para que los recuerden, los tipos de triángulos que existen:

(Fig. 5) Tipos de Triángulos

Volviendo a los CPs más sencillos, la figura 2 muestra la Mediatriz. La mediatriz corta el lado del cuadrado en dos, generando dos rectángulos, cada uno con un área que es la mitad del área del cuadrado original.

(Fig.6) Rectángulos

Ahora, tomemos una hoja de papel cuadrada y hagamos Origami (o sea, doblar papel en Japonés). ¡Doblemos el CP1! Entonces, la primera pregunta que nos hacemos es:

ACERTIJO NO.1

¿En qué dirección lo doblamos?

He querido resaltar esta pregunta debido a su importancia fundamental. La dirección del doblez es el primero de los grandes acertijos en la resolución de CPs. Para cada línea en un CP solo hay dos opciones de doblado hacia adelante o hacia atrás; pocas, ¡pero hay que DECIDIR!. Esta ambigüedad yo la llamo la PRIMERA INCERTIDUMBRE ESPACIAL: el CP no nos da la certeza de la dirección de doblado. Sin embargo, antes de analizar con detenimiento la primera incertidumbre espacial debemos establecer algunos elementos básicos más.

Aunque relativamente poco frecuente, algunos creadores de origami nos muestran el CP con el primero de los acertijos resuelto, pues nos indican la dirección de cada doblez. En este caso el CP se denomina CPMV que significa CP CON MONTAÑAS Y VALLES ASIGNADOS. Veamos con los CPs más sencillos a que nos referimos. Vamos a dibujar los dos CPMV de la diagonal. Para ello utilizamos la notación simbólica del origami:

(Fig.7) CPMV: en valle ____ (Fig.8) CPMV: en montaña

Entonces, las figuras tres y cuatro nos indican la dirección de los dobleces, la primera en valle y la segunda en montaña. Veamos ahora los diagramas de estos CPMV:

(Fig.9) Diagrama en valle_____ (Fig.10) Diagrama en montaña

Como pueden ver, para obtener los diagramas solo añadí las flechas. Ahora se leen así: para la figura 8 "doblar en la diagonal hacia adelante" y para la figura 9: "doblar en la diagonal hacia atrás" . ¡Hagámoslo con el papel! Si el papel es de dos colores, tendremos que considerar, si queremos el color seleccionado por dentro o por fuera. Pero, por ahora no consideraremos esta variable y pensaremos que el papel es del mismo color por ambos lados.

Bien, ¡ya lo hicimos!. Como pueden observar, para el caso de una sola línea es indiferente la dirección del doblez. ¡Trivial por ahora!

Todo lo que hemos escrito hasta ahora sirve también y de la misma manera para el CP de la mediatriz. Para ambos CPs, bisectriz o mediatriz, y para ambas líneas, valle o montaña, las figuras obtenidas se muestra en los siguientes diagramas:

(Fig.11) Triángulo rectángulo isósceles __(Fig.12) Rectángulo

Hemos obtenido estas dos figuras geométricas básicas y me gustaría con ellas indicarles un concepto más en la resolución de CPs. Si consideramos el papel como el plano, entonces estas figuras son realmente tridimensionales; sin embargo, lo común en origami es decir que son planas. Por lo tanto, me gusta llamarlas FIGURAS PLANAS MULTICAPAS, para diferenciarlas del plano; pero también, para diferenciarlas de las figuras de origami que si son propiamente tridimensionales, las cuales se llaman FIGURAS 3D.

Si los CPs son como los embriones de los modelos de origami; de seguro, la bisectriz o la mediatriz serían la columna vertebral. Son líneas "estructuralmente importantes" y son, a mi parecer, las primeras referencias en resolución de CPs. Sobre referencias ya nos dedicaremos bastante más adelante. Por ahora nos preguntaremos:

¿Qué sucederá con los CPs más sencillos si les incorporamos una nueva línea? ¿Qué variables y acertijos se nos propondrán como retos? Tengamos paciencia, que andando despacio se llega largo y seguro.

En este blog tus comentarios son extremadamente importantes; por favor escribirlos abajo. Si no tienes una cuenta ni un password no se preocupe, toque donde dice anónimo y allí puede escribir su mensaje.

Si deseas una copia en formato pdf de este documento solicítamelo a la dirección eric@internetelfaro.com que con mucho gusto te lo enviaré

Hasta dentro de 15 días.....