...EN CARACTERES MATEMATICOS

INTROITO

Estimados lectores:

¡Mea culpa! No he podido cumplir con el compromiso de entregar la segunda parte de la entrada anterior en una semana. Realmente la que les ofrezco ahora, es bastante compleja y me tomó mucho tiempo elaborarla. Más del que yo esperaba. Pero aquí está y espero que con ella aprendan muchas cosas sobre la resolución de CPs. De este modo completamos la entrada total con el nombre:

"LA NATURALEZA ESTA ESCRITA EN CARACTERES MATEMATICOS"

Atentamente,

Ing. Eric Madrigal
Asociación Costarricense de origami


III PARTE

MATEMATICAS EN HUANCAVELICA

1. LA BUSQUEDA DEL TESORO

Al finalizar la entrada anterior nos preguntamos sobre el cómo ubicamos cosas en el espacio. Para ello, los invito a tomar un avión virtual y dirigirnos a la ciudad de Lima en Perú. De allí tomaremos un autobús que nos llevará directamente a la pintoresca ciudad de Huancavelica enclavada en las serranías de la cordillera de los Andes.

Nuestro objetivo es encontrarnos con el origamista peruano Alejandro Dueñas quien nos ha solicitado una especial ayuda. Parece ser que hace unos días atrás, unos Apus, o dioses de las montañas, le quitaron un CP muy valioso de su propiedad y lo dejaron en algún lugar de la ciudad. Este CP, nos indica Alejandro, contiene un código secreto que le permitirá llegar a encontrar un valiosísimo tesoro.

Hemos llegado ya a Huancavelina y estamos con Alejandro en algún lugar de su ciudad; y nos pregunta: ¿Donde estará mi CP?

Dado que viniendo de la estación de autobús hemos visto el CP cerca del correo vamos a ayudar a Alejandro a encontrarlo.

Para ello sacamos de nuestra caja de herramientas el visualizador de direcciones: el sistema de ejes cartesianos.

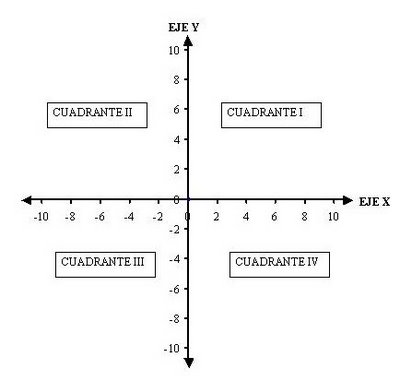
El sistema consta de dos ejes, el eje X que va horizontalmente y el eje Y que va verticalmente. Los ejes están a 90º uno respecto del otro y se cruzan en los que se llama el origen o punto cero. Los ejes están marcados como una regla para medir y sus marcas dependen sistema de medidas que estemos usando (metros, pulgadas, etc). Las escalas pueden cambiar a conveniencia. Si nos movemos del origen a la izquierda o hacia abajo, los valores serán negativos y hacia la derecha o arriba los valores serán positivos. Al cruzarse los ejes, se forman cuatro cuadrantes tal como se ve en la figura.

Entonces, con nuestros ejes, vamos a ayudar a Alejandro. Veamos:

-"Alejandro, viniendo de la estación del autobús, hemos visto tu CP junto a la oficina de correos. Te damos la dirección: De esta esquina donde estamos conversando, camina 150 metros al norte, hasta llegar a la otra esquina del parque, de allí caminas 150 metros al oeste y llegas a la esquina de la iglesia. Luego debes ir 100 metros al norte y allí, a tu derecha encontrarás tu CP."- "Esperamos que cuando lo encuentres compartas tu tesoro con nosotros"-

Mientras Alejandro va a buscar su CP, resolvamos las siguientes interrogantes: ¿cuántos metros debe recorrer Alejandro para encontrar su CP? y, si no existiesen edificios ni otros obstáculos, ¿cuántos metros debería recorrer? La segunda pregunta nos indica algo muy importante de la geometría: la distancia más corta entre dos puntos del espacio plano es siempre una línea recta. Veámoslo en los ejes cartesianos a los que hemos quitado los cuadrantes que no nos son de utilidad:

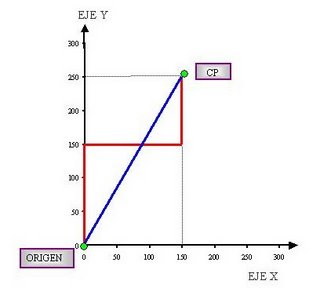
La línea roja representa, por lo tanto, lo que camina realmente Alejandro; o sea, 150m + 150m + 100m = 400 m. La línea azul representa la distancia real que hay entre nosotros y el CP y que es la distancia más corta si no existiesen obstáculos. ¿Cuánto mide esta distancia? Para resolver esta interrogante debemos recurrir a un antiguo matemático griego: PITAGORAS y a su famoso teorema. En la siguiente figura, observamos que la línea azul forma con el eje X y la proyección del eje Y un triángulo rectángulo, que es precisamente lo que necesitamos para aplicar el teorema de Pitágoras:

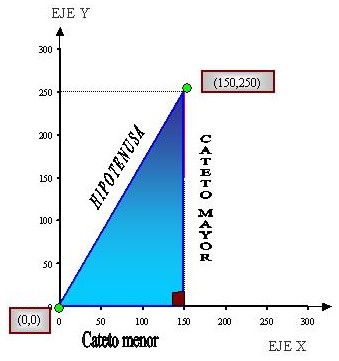
He puesto los nombres de acuerdo a los conceptos matemáticos. La hipotenusa (h) corresponde al segmento opuesto al ángulo de 90º y los catetos son, por supuesto, los segmentos adyacentes (recordar que si el triángulo rectángulo es además isósceles, ambos catetos miden los mismo). Entonces el teorema de Pitágoras dice:

"EN UN TRIANGULO RECTANGULO EL CUADRADO DE LA HIPOTENUSA ES IGUAL A LA SUMA DE LOS CUADRADOS DE LOS CATETOS"

Para ubicar los puntos verdes dentro del sistema de ejes cartesianos se utiliza lo que se llaman COORDENADAS CARTESIANAS; o sea, el valor en el eje X y el valor en el eje Y y se escriben con el siguiente formato (x,y). De esta manera para el lugar donde estamos hablando, las coordenadas serían (0,0) y para el lugar donde se encuentra el CP las coordenadas son (150,250). Veámoslo de una manera más clara:

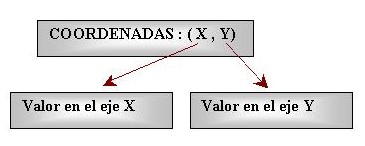
Si sustituimos los valores correspondientes para X= cateto menor = 150 y Y= cateto mayor = 250, obtendremos los siguientes cálculos:

Si comparamos lo que ha tenido Alejandro que recorrer de 400 m para llegar al CP, con la distancia real de 292 m, vemos que hay un ahorro importante de distancia si tan solo pudiésemos brincarnos los objetos.

2. LAS PISTAS PARA LA BUSQUEDA

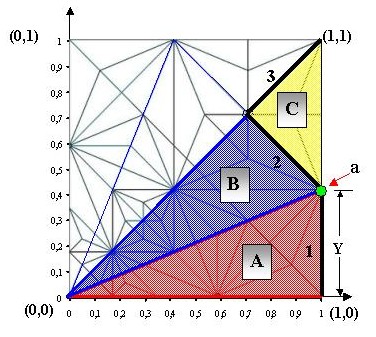
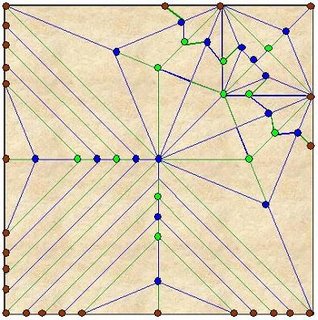
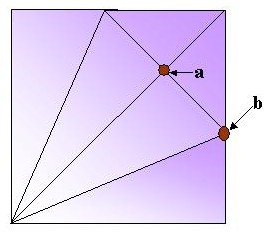
Bueno, aquí ya ha llegado Alejandro con su CP y nos pide que le ayudemos a indagar dos puntos de su CP con los cuales podría abrir la primera de las puertas que lo separan de su tesoro. Veamos el CP donde Alejandro ha marcado los puntos de su interés:

Es realmente un CP muy hermoso con simetría en la diagonal.

De la misma manera como se dan direcciones en una ciudad, podemos dar direcciones en un CP; por lo tanto vamos a ubicar nuestro CP en un sistema de ejes cartesianos y además vamos a hacer coincidir los lados con los ejes. Le añadiremos también las coordenadas de las esquinas. Veamos:

Debemos observar que se ha modificado la escala de los ejes a conveniencia, lo cual es matemáticamente correcto. Al hacer que el CP tenga un valor unitario significa que sus cálculos son los mismo para cualquier papel que estemos utilizando.

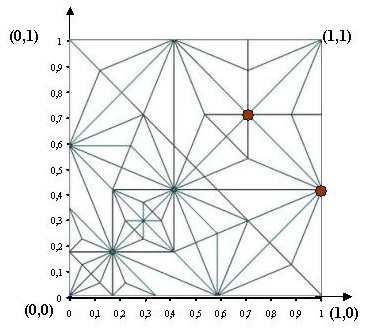
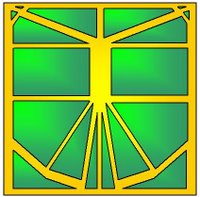
Muy bien, ahora sí tenemos todos los recursos necesarios para ayudar a Alejandro. Es claro que el CP, que en realidad es un CPMV, es bastante complejo con muchos rayos y nodos pero no debemos dejarnos confundir. Decía Santo Tomás de Aquino, que una de las formas básicas del aprendizaje consiste en dejar de lado las cosas muy complejas y fijar nuestra atención en las más fundamentales. Si aplicamos este principio y además somos buenos observadores y además leímos la entrada anterior, nos daremos cuenta de que entre el CP de Alejandro y el diseño del CP de la base cometa con que concluimos la entrada anterior, hay una íntima relación. Pongámoslos juntos para verlos:

O sea que, ayudarle a Alejandro a encontrar los puntos a y b es lo mismo que hacerlo en una base cometa como la que mostramos.

Antes de ubicar a y b quisiera sacar una conclusión importante de todo lo que hemos estado analizando:

"En un CP los rayos tienen medida y responden a la pregunta ¿cuánto mide? y los nodos tienen ubicación y responden a la pregunta ¿cuáles son las coordenadas?"

Dado que el CP de Alejandro tiene simetría en la diagonal, me gustaría que nos preguntásemos ¿cuánto mide la diagonal? Aplicando el principio de Santo Tomás, dejemos de lado las demás líneas y enfoquémonos solamente en la diagonal:

La diagonal junto con los ejes forma un triángulo rectángulo isósceles puesto que estamos utilizando un papel cuadrado. Además la diagonal es la hipotenusa. Por lo tanto, calculando con el teorema de Pitágoras tenemos:

Entonces el rayo que llamamos diagonal se inicia en (0,0), termina en (1,1) y mide:
. Si tuviéramos un papel de 20 cm entonces la diagonal se inicia en (0,0), termina en (20,20) y mide 20 x . Del mismo modo para cualquier tamaño de papel.

Ahora resolvamos el punto a.

Resolver el punto a significa, como ya lo hemos establecido, encontrar sus coordenadas. El punto a con sus ejes conforman el triángulo rectángulo A en rojo. Con respecto al eje X no hay problema pues su valor es 1, pero tenemos que determinar el valor de Y. Para ello consideremos lo siguiente:

1. El triángulo A es imagen especular del triángulo azul B, tal y como se podría comprobar doblando el papel.

2. El triángulo C es un triángulo isósceles, lo cual, también se puede comprobar doblando papel.

Por lo tanto los segmentos 1, 2, 3 marcados con negro son todos iguales. Entonces basta con saber el valor de uno de ellos para conocer el valor de los otros. Creo que la forma más fácil es calcular el segmento que coincide con la diagonal.

Entonces, dado que la diagonal mide y si doblamos el lado que mide 1 sobre ella, entonces el segmento 3 mide: -1 y los otros dos segmentos miden igual. Por lo tanto, la distancia Y mide:

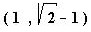Tenemos ya las coordenadas del punto a: . Con los valores de las coordenadas y aplicando el Teorema de Pitágoras obtendremos que la medida del rayo que va desde el origen al punto a es de:

¡Número realmente raro! Este rayo es bisectriz del ángulo de 45º como vimos en la entrada anterior.

Ahora averigüemos el punto b:

Para el punto b, debemos notar que sus coordenadas forman un triángulo rectángulo isósceles. Por lo tanto, los catetos miden lo mismo. Además su distancia al origen, que es la hipotenusa, tiene valor de 1 lo cual comprobamos con solo doblar el lado sobre la diagonal. Utilizando el Teorema de Pitágoras resolvemos:

Por lo tanto, las coordenadas del nodo b son: y el rayo que lo une con el origen mide 1. Con esto hemos terminado y ya le podemos dar el CP a Alejandro con los puntos localizados.

3. EL TESORO DE ALEJANDRO

"Toma, Alejandro, aquí esta tu CP con las coordenadas que nos pediste"

"¡Muchas gracias!, Ahora si podré abrir todas las puertas para llegar al tesoro."

"¿Nos mostrarás el tesoro?"

"¡Por supuesto!, ¡un momento!, ¡listo! Solo toquen donde dice BASE COLAPSADA"

BASE COLAPSADA

Bueno, lectores, como ustedes ya habrán entendido, todo lo que hemos hecho con el CP de Alejandro Dueñas, sirve para la BASE COMETA o cualquier CP que utilice sus referencias. Los puntos o nodos a y b son dos referencias que se derivan de los conceptos de la base cometa. Cada base, sea tradicional o contemporánea, tendrá sus propias referencias.

Nuestro siguiente paso será, por supuesto, tratar con la siguiente base del origami japonés: LA BASE DEL PEZ.

En este blog tus comentarios son extremadamente importantes; por favor escribirlos abajo. Si no tienes una cuenta ni un password no se preocupe, toque donde dice anónimo y allí puede escribir su mensaje.Si deseas una copia en formato pdf de este documento solicítamelo a la dirección eric@internetelfaro.com que con mucho gusto te lo enviaré.

Hasta dentro de una semana...

LA NATURALEZA ESTA ESCRITA . . .

INTROITO

Estimados lectores:

Lastimosamente me fue imposible completar la entrada tal como quería entregárselas. La verdad es que en estos quince días estuve algo enfermo. Por lo tanto, he tenido que dividir la entrada en dos y me comprometo a entregar la otra parte en una semana. Esto hizo que también dividiera el título, pero se que muchos sabrán como es la continuación. Les recuerdo a los nuevos lectores que antes de leer esta entrada deben remitirse a las entradas anteriores pues todo va debidamente concatenado. Felicito a los que por su cuenta descubrieron el significado del logo. Si desean saber más solo toquen la siguiente imagen:

Espero que sigan disfrutando la lectura de mi blog y les recuerdo lo importante que es que escriban sus comentarios.

Atentamente,

Ing. Eric Madrigal
Asociación Costarricense de Origami

Nota: algunas palabras o frases aparecerán en verde.Esto significa que
son añadidos ulteriores a la publicaciónde la entrada y por sugerencia
directa de los lectores.

I PARTE

CONSTELACIONES

En la entrada anterior introducimos los conceptos de rayos y nodos o vértices. Las líneas de un CP se cruzan en la superficie del papel generando así intersecciones que se denominan nodos y las líneas que los forman quedan divididas en segmentos que irradian desde el nodo y que llamamos rayos. Me gustaría que mantengamos estos conceptos frescos en nuestra mente.

Durante las últimas décadas, el origami ha ido, poco a poco, elaborando todo un lenguaje simbólico que nos permite interpretar adecuadamente todas las acciones que debemos realizar al doblar un papel. Uno de estos simbolismos es el de la líneas. Los diagramas de origami usan varios tipos de líneas: valle, montaña, marca, rayos X, etc. En cambio, en la teoría de los CPs usamos solamente tres tipos diferentes de líneas para obtener los CPMV; y con un cambio bastante importante. Las líneas tradicionales de guiones y puntos son sustituidas por líneas de colores. En el libro ODS, Robert Lang establece que líneas coloreadas gruesas representan valles; líneas negras gruesas, representan montañas y líneas negras delgadas, representan marcas. En este blog, y solo por consideraciones de claridad didáctica utilizaremos el código de colores que aparece en el siguiente cuadro:

Dado que tendemos a olvidarnos constantemente de estas convenciones, me gustaría ofrecerles el siguiente recurso memorístico:

MICROCUENTO

SOBRE LA LLEGADA DEL ORIGAMI A AMERICA

Veíamos, con asombro, a la distancia, correr por aquel irreverente valle, el torrentoso río de aguas azules, (¡cómo el cielo que te cubre, amada América!-le dije); y en las montañas, igual que loros vestidos de jade, colgando, las tremulantes selvas indígenas con su amasijo vegetal siempreverde. Y nos preguntabamos, ¿cómo, barquito de papel, lograste no sucumbir al embate de tu alma aventurera? ¿No era mejor que te quedaras tranquilo en el mediterránico océano de tu Sphera Mundi? Pero, ¡aquí estás, desde antaño!¡Para quedarte!Y eso basta.

En homenaje a los increíbles

origamistas latinoamericanos

Espero que con esto, cuando lean este blog, nunca se les olvide el significado de los colores de las líneas: valle con azul, montaña con verde.

Ahora bien, con respecto a los nodos, vamos a incluir sobre las intersecciones, pequeños círculos de colores, también verdes y azules. Sobre el significado de estos colores trataremos más adelante. Unicamente me gustaría indicarles que cuando a un CP se le dibujan los nodos, entonces se llama VACP (de las siglas en inglés para Vertex Assigned Crease Pattern).

Veamos un ejemplo muy sencillo de CP con líneas y nodos de colores:

Fig.1: Líneas tradicionales____Fig. 2: Líneas coloreadas

Hace unos días, estaba trabajando sobre un CPMV y le había marcado todas las líneas y los nodos de colores cuando entró un amigo mío de once años llamado Kevin. Al ver el CP sobre el escritorio y sin saber lo que era, solamente exclamó: "Mirá!, parecen constelaciones". Efectivamente, los CPS, con sus rayos y nodos, parecen dibujos antiguos de hermosas constelaciones.

Ahora desearía que apagáramos las luces virtuales, y en la oscuridad dirijamos nuestra mirada al vasto y oscuro universo y allí descubramos la CONSTELACION DEL GANSO:

Fig. 3: Constelación del Ganso

Este hermoso CP fue diseñado por el joven origamista peruano Elerth Leiva y tuvo la dicha de inspirar al famoso origamista uruguayo Román Díaz a realizar una genial interpretación del CP y lograr un hermoso modelo final. Si tocamos sobre la Constelación, aparecerá el modelo terminado de Román para el CP de Elerth.

Para terminar esta parte, deseo mostrarles con todo su esplendor el VACP y la base colapsada del modelo del Ganso de Elerth.

Fig.4: VACP de la base del Ganso

Fig. 5: Base colapsada del Ganso

Si tocan el CP obtendrán la foto del ganso original, tal y como salió de la mente de Elerth y si tocan la figura de la base colapsada serán dirigidos a un documento en formato pdf con un entrevista muy buena a Elerth Leiva.


II PARTE

LA BASE COMETA O LA ESTRUCTURACIÓN DEL MISTERIO

La primera y más sencilla de las BASES TRADICIONALES del Origami Japonés es la BASE COMETA. Veamos su CP, su CPMV , su CPD y la BASE colapsada:

Fig. 6: CP _____________Fig.7: MVCP

Fig.8: CPD_____________Fig. 9: Base colapsada

La base Cometa es simétrica con respecto a la bisectriz. El CP consta de tres rayos que irradian del origen, el central es la diagonal y los otros dos intersectan dos lados del cuadrado. El CPMV muestra dos rayos en valle y una línea de marca central. Cada mitad simétrica consta de dos triángulos, un triángulo rectángulo escaleno y un triángulo obtusángulo escaleno, por lo tanto son cuatro triángulo como se ve en el CPD. La base colapsada nos recuerda los cometas (papalotes, barriletes, etc, dependiendo del país de origen del lector) y en inglés se denomina KITE. Esta figura geométrica es definida como un cuadrilátero con dos pares de lados adyacentes iguales. Veamos:

Un ejercicio interesante que tiene maravillosas consecuencias es trazar la línea que une las dos intersecciones de las líneas con los lados:

Esta línea, que es perpendicular a la diagonal, divide el triángulo obtuso en dos triángulos, un triángulo rectángulo escaleno (b) y un triángulo rectángulo isósceles (c). Lo interesante es notar que el triángulo b es la imagen especular del triángulo a; o sea, es como si el triángulo a se viese en un espejo. Muchos cálculos matemáticos en la resolución de CPs se basan en este tipo de sorprendentes relaciones que ocurren al doblar el papel.

Ahora debemos preguntarnos: ¿Qué hace, realmente, en el papel la base cometa? ¿Cuál es su objetivo? En la entrada anterior vimos que las bisectrices dividen los ángulos rectos opuestos a la mitad, o sea, en ángulos de 45º y si doblamos el papel, obtenemos dos puntas de 45º opuestas y con dos capas de papel. Sin embargo, para el origami estas puntas no son realmente muy versátiles aunque de hecho superan a las puntas del cuadrado de 90º.

El ingenio de los primeros origamistas japoneses pronto se las ideó para crear una punta que fuese más versátil. Para ello procedieron de la siguiente manera:

1. Marcaron en el papel cuadrado la bisectriz

2. Llevaron uno de los lados a reposar sobre la bisectriz. Veamos lo que ocurre:

Fig. 10: Angulo alfa

¿Cuánto mide el ángulo alfa? Para saberlo debemos percatarnos que la nueva línea formada es también una bisectriz del ángulo de 45º. Por lo tanto, el nuevo ángulo es de 45º/2 que es 22.5º. El ángulo alfa es por tanto de 45º + 22.5º = 67.5º. Además debemos observar que la figura generada es un trapecio rectángulo. Rotemos la figura y veámoslo:

Fig. 11: Trapecio rectángulo

3. Llevaron el otro lado adyacente sobre la diagonal. Veamos:

Fig. 12: Nuevo ángulo alfa

Dado que el nuevo doblez es también una bisectriz del otro ángulo de 45º, el nuevo ángulo alfa es la suma de dos ángulos de 22.5º; o sea, es un ángulo de 45º.

¡Perfecto! ¿Cuál es la conclusión? Los japoneses lograron con la base Cometa generar una punta de 45º pero centrada en la diagonal. Si observamos el CP de la base Cometa nos percatamos, entonces, que el ángulo original de 90º ha sido dividido en cuatro ángulos iguales de 22.5º:

Fig. 13: CP con ángulos de 22.5º

Para tener una mejor perspectiva de la punta generada doblemos la base cometa por la diagonal. Veamos:

Fig. 14: Base Cometa doblada en la diagonal

Hasta este punto, surge una nueva pregunta: ¿que función cumple la diagonal o bisectriz en la base Cometa? Al colapsar la base, esta línea queda solamente como una marca, por lo tanto, ¿será realmente importante? La respuesta a esta interrogante es un rotundo SI; es más, la bisectriz no solo es importante sino que es fundamental. Para probarlo, los invito a imprimir los siguientes CPs y colapsarlos. Solo uno de ellos es la base Cometa.

Fig. 15: ¿Cuál será la base cometa?

La bisectriz es en la base Cometa la respuesta a una de las interrogantes más importantes que nos hacemos al resolver CPs:

2do Acertijo

¿Cuáles son las referencias?

Tradicionalmente se habla de puntos de referencia, pero, personalmente prefiero utilizar la palabra llana REFERENCIAS pues algunas veces serán puntos en el plano, pero en otras serán líneas. ¿Qué son, entonces, las referencias? Todo el proceso de resolución de CPs se basa en saber con exactitud donde van colocadas cada una de las líneas. Aquí no existe un "más o menos por el centro". La línea pasa por el centro exactamente o no pasa por el centro. La resolución de CPs es realmente un pasatiempo de exactitud y no podría ser de otra manera: con la cantidad de dobleces en un espacio tan reducido, todo debe quedar exactamente colocado en su lugar.

Para lograr establecer la posición de las líneas es necesario que exista una referencia; por ejemplo, si nos dicen: haga una marca a la mitad de un lado y luego lleve una punta hasta esa marca, entonces, ¿me entienden? , la marca sobre el lado es una referencia.

Al realizar la base cometa, se nos indica que debemos llevar el lado sobre la diagonal. Por lo tanto, la diagonal es una referencia. Es la referencia principal y única de la base cometa. Cada CP tendrá sus propias referencias las cuales debe ser averiguadas. Para determinar referencias se requiere del mayor esfuerzo e ingenio posible; y se vale de todo: métodos netamente origámicos, métodos matemáticos, regla y compás, o una mezcla de todos. Lo importante: determinar las referencias.

Me gustaría indicar que en el procedimiento de resolución de CPs es bastante común, imprimir el CP y sobre él empezar a jugar con las líneas para ver si son valles y montañas y lograr de este modo colapsar la base. Para mi y este blog, este es solamente el principio de la resolución. El CP impreso es algo así como la herramienta básica de trabajo pero no es el edificio que debe construirse. El verdadero edificio es la base colapsada. La base colapsada, desde mi punto de vista, será debidamente construída cuando a partir de cualquier tamaño de papel la logremos obtener y para esto, es fundamental encontrar las referencias para dar la ubicación exacta de cada doblez del CP.

Volvamos al CP de la base Cometa, pero utilicemos el diseño donde aparece la perpendicular a la diagonal. Muchas veces, la base cometa sirve de paso hacia modelos más complejos y las referencias de éstos, se encuentran en ella. Por lo tanto, debemos tener bien ubicados todos sus nodos. Particularmente nos referimos a los puntos a y b en la siguiente figura:

Fig. 16: Base Cometa con nodos a y b

La determinación de estos dos nodos nos lleva directamente a adentrarnos en el mágico mundo de las matemáticas de una manera más profunda y se hace necesario que introduzcamos varios conceptos más. La pregunta principal es, ¿cómo ubicamos cosas en el espacio?

En este blog tus comentarios son extremadamente importantes; por favor escribirlos abajo. Si no tienes una cuenta ni un password no se preocupe, toque donde dice anónimo y allí puede escribir su mensaje.Si deseas una copia en formato pdf de este documento solicítamelo a la dirección eric@internetelfaro.com que con mucho gusto te lo enviaré.

Hasta dentro de una semana...