LA NATURALEZA ESTA ESCRITA . . .
INTROITO
Estimados lectores:
Atentamente,
Ing. Eric Madrigal
Asociación Costarricense de Origami
Nota: algunas palabras o frases aparecerán en verde.Esto significa que
son añadidos ulteriores a la publicaciónde la entrada y por sugerencia
directa de los lectores.
I PARTE
En la entrada anterior introducimos los conceptos de rayos y nodos o vértices. Las líneas de un CP se cruzan en la superficie del papel generando así intersecciones que se denominan nodos y las líneas que los forman quedan divididas en segmentos que irradian desde el nodo y que llamamos rayos. Me gustaría que mantengamos estos conceptos frescos en nuestra mente.
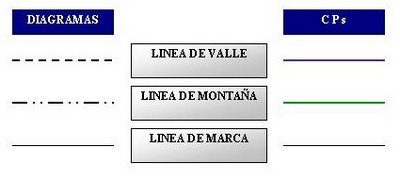
Durante las últimas décadas, el origami ha ido, poco a poco, elaborando todo un lenguaje simbólico que nos permite interpretar adecuadamente todas las acciones que debemos realizar al doblar un papel. Uno de estos simbolismos es el de la líneas. Los diagramas de origami usan varios tipos de líneas: valle, montaña, marca, rayos X, etc. En cambio, en la teoría de los CPs usamos solamente tres tipos diferentes de líneas para obtener los CPMV; y con un cambio bastante importante. Las líneas tradicionales de guiones y puntos son sustituidas por líneas de colores. En el libro ODS, Robert Lang establece que líneas coloreadas gruesas representan valles; líneas negras gruesas, representan montañas y líneas negras delgadas, representan marcas. En este blog, y solo por consideraciones de claridad didáctica utilizaremos el código de colores que aparece en el siguiente cuadro:
MICROCUENTO
Veíamos, con asombro, a la distancia, correr por aquel irreverente valle, el torrentoso río de aguas azules, (¡cómo el cielo que te cubre, amada América!-le dije); y en las montañas, igual que loros vestidos de jade, colgando, las tremulantes selvas indígenas con su amasijo vegetal siempreverde. Y nos preguntabamos, ¿cómo, barquito de papel, lograste no sucumbir al embate de tu alma aventurera? ¿No era mejor que te quedaras tranquilo en el mediterránico océano de tu Sphera Mundi? Pero, ¡aquí estás, desde antaño!¡Para quedarte!Y eso basta.
En homenaje a los increíbles
Ahora bien, con respecto a los nodos, vamos a incluir sobre las intersecciones, pequeños círculos de colores, también verdes y azules. Sobre el significado de estos colores trataremos más adelante. Unicamente me gustaría indicarles que cuando a un CP se le dibujan los nodos, entonces se llama VACP (de las siglas en inglés para Vertex Assigned Crease Pattern).
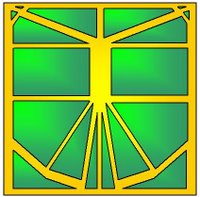
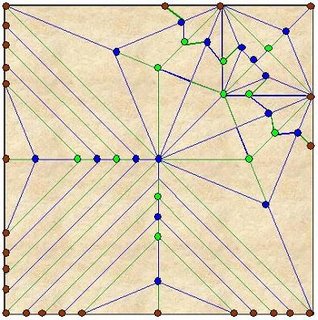
Hace unos días, estaba trabajando sobre un CPMV y le había marcado todas las líneas y los nodos de colores cuando entró un amigo mío de once años llamado Kevin. Al ver el CP sobre el escritorio y sin saber lo que era, solamente exclamó: "Mirá!, parecen constelaciones". Efectivamente, los CPS, con sus rayos y nodos, parecen dibujos antiguos de hermosas constelaciones.
Este hermoso CP fue diseñado por el joven origamista peruano Elerth Leiva y tuvo la dicha de inspirar al famoso origamista uruguayo Román Díaz a realizar una genial interpretación del CP y lograr un hermoso modelo final. Si tocamos sobre la Constelación, aparecerá el modelo terminado de Román para el CP de Elerth.
Para terminar esta parte, deseo mostrarles con todo su esplendor el VACP y la base colapsada del modelo del Ganso de Elerth.
Fig.4: VACP de la base del Ganso
Fig. 5: Base colapsada del Ganso
II PARTE
La primera y más sencilla de las BASES TRADICIONALES del Origami Japonés es la BASE COMETA. Veamos su CP, su CPMV , su CPD y la BASE colapsada:
Fig.8: CPD_____________Fig. 9: Base colapsada
La base Cometa es simétrica con respecto a la bisectriz. El CP consta de tres rayos que irradian del origen, el central es la diagonal y los otros dos intersectan dos lados del cuadrado. El CPMV muestra dos rayos en valle y una línea de marca central. Cada mitad simétrica consta de dos triángulos, un triángulo rectángulo escaleno y un triángulo obtusángulo escaleno, por lo tanto son cuatro triángulo como se ve en el CPD. La base colapsada nos recuerda los cometas (papalotes, barriletes, etc, dependiendo del país de origen del lector) y en inglés se denomina KITE. Esta figura geométrica es definida como un cuadrilátero con dos pares de lados adyacentes iguales. Veamos:
Un ejercicio interesante que tiene maravillosas consecuencias es trazar la línea que une las dos intersecciones de las líneas con los lados:
Esta línea, que es perpendicular a la diagonal, divide el triángulo obtuso en dos triángulos, un triángulo rectángulo escaleno (b) y un triángulo rectángulo isósceles (c). Lo interesante es notar que el triángulo b es la imagen especular del triángulo a; o sea, es como si el triángulo a se viese en un espejo. Muchos cálculos matemáticos en la resolución de CPs se basan en este tipo de sorprendentes relaciones que ocurren al doblar el papel.
Ahora debemos preguntarnos: ¿Qué hace, realmente, en el papel la base cometa? ¿Cuál es su objetivo? En la entrada anterior vimos que las bisectrices dividen los ángulos rectos opuestos a la mitad, o sea, en ángulos de 45º y si doblamos el papel, obtenemos dos puntas de 45º opuestas y con dos capas de papel. Sin embargo, para el origami estas puntas no son realmente muy versátiles aunque de hecho superan a las puntas del cuadrado de 90º.
El ingenio de los primeros origamistas japoneses pronto se las ideó para crear una punta que fuese más versátil. Para ello procedieron de la siguiente manera:
1. Marcaron en el papel cuadrado la bisectriz
2. Llevaron uno de los lados a reposar sobre la bisectriz. Veamos lo que ocurre:
Fig. 10: Angulo alfa
¿Cuánto mide el ángulo alfa? Para saberlo debemos percatarnos que la nueva línea formada es también una bisectriz del ángulo de 45º. Por lo tanto, el nuevo ángulo es de 45º/2 que es 22.5º. El ángulo alfa es por tanto de 45º + 22.5º = 67.5º. Además debemos observar que la figura generada es un trapecio rectángulo. Rotemos la figura y veámoslo:
Fig. 11: Trapecio rectángulo
3. Llevaron el otro lado adyacente sobre la diagonal. Veamos:
Fig. 12: Nuevo ángulo alfa
Dado que el nuevo doblez es también una bisectriz del otro ángulo de 45º, el nuevo ángulo alfa es la suma de dos ángulos de 22.5º; o sea, es un ángulo de 45º.
¡Perfecto! ¿Cuál es la conclusión? Los japoneses lograron con la base Cometa generar una punta de 45º pero centrada en la diagonal. Si observamos el CP de la base Cometa nos percatamos, entonces, que el ángulo original de 90º ha sido dividido en cuatro ángulos iguales de 22.5º:
Fig. 13: CP con ángulos de 22.5º
Fig. 14: Base Cometa doblada en la diagonal
Fig. 15: ¿Cuál será la base cometa?
Tradicionalmente se habla de puntos de referencia, pero, personalmente prefiero utilizar la palabra llana REFERENCIAS pues algunas veces serán puntos en el plano, pero en otras serán líneas. ¿Qué son, entonces, las referencias? Todo el proceso de resolución de CPs se basa en saber con exactitud donde van colocadas cada una de las líneas. Aquí no existe un "más o menos por el centro". La línea pasa por el centro exactamente o no pasa por el centro. La resolución de CPs es realmente un pasatiempo de exactitud y no podría ser de otra manera: con la cantidad de dobleces en un espacio tan reducido, todo debe quedar exactamente colocado en su lugar.
Para lograr establecer la posición de las líneas es necesario que exista una referencia; por ejemplo, si nos dicen: haga una marca a la mitad de un lado y luego lleve una punta hasta esa marca, entonces, ¿me entienden? , la marca sobre el lado es una referencia.
Al realizar la base cometa, se nos indica que debemos llevar el lado sobre la diagonal. Por lo tanto, la diagonal es una referencia. Es la referencia principal y única de la base cometa. Cada CP tendrá sus propias referencias las cuales debe ser averiguadas. Para determinar referencias se requiere del mayor esfuerzo e ingenio posible; y se vale de todo: métodos netamente origámicos, métodos matemáticos, regla y compás, o una mezcla de todos. Lo importante: determinar las referencias.
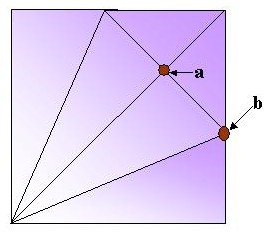
Volvamos al CP de la base Cometa, pero utilicemos el diseño donde aparece la perpendicular a la diagonal. Muchas veces, la base cometa sirve de paso hacia modelos más complejos y las referencias de éstos, se encuentran en ella. Por lo tanto, debemos tener bien ubicados todos sus nodos. Particularmente nos referimos a los puntos a y b en la siguiente figura:
Fig. 16: Base Cometa con nodos a y b
En este blog tus comentarios son extremadamente importantes; por favor escribirlos abajo. Si no tienes una cuenta ni un password no se preocupe, toque donde dice anónimo y allí puede escribir su mensaje.Si deseas una copia en formato pdf de este documento solicítamelo a la dirección eric@internetelfaro.com que con mucho gusto te lo enviaré.
Hasta dentro de una semana...














3 Comentarios:
Sin duda un Blog maravilloso para los que no se conforman con dolar diagramas. Me gusto la experiencia de poder ayudarte y agradesco que me haz hechoi particite de tu trabajo.
Gracias Eric.
Y suerte con las figuritas.. y con las proximas entradas!!!
¡Madrigal! ¿qué digo?: ¡Magistral!
Todo excelente, amigo Eric. En lo particular, quedo esperando ya el siguiente capítulo.
¡Gracias por tu enorme empeño y entusiasmo!
Atentamente:
Fernando García Ramírez,
desde Tepic, Nayarit, México.
P. D.- ¡Felicidades asimismo por la entrevista que hiciste al joven amigo!
Elerth: también para ti: ¡Muchas felicidades!
muy interesante... y ahora a devorar el siguiente pedacito!
Un saludo desde Chile!
Publicar un comentario
Suscribirse a Comentarios de la entrada [Atom]
<< Página Principal