UN PASATIEMPO DE DECISIONES

INTROITO

Estimados lectores: cumpliendo con mi compromiso de entregas cada 15 días, aquí coloco a su consideración la segunda entrada de mi blog. Les recuerdo que son mis notas de como voy aprendiendo todo lo relacionado con resolución de CPs. Pido disculpas por los errores que cometo, especialmente relacionados con los dibujos, el manejo del lenguaje html y de las imágenes que aún estoy en proceso de dominar. ¡Cada día aprendo más!

Atentamente,

Eric Madrigal
ACRO

Nota: algunas palabras o frases aparecerán en verde.
Esto significa que son añadidos ulteriores a la publicación
de la entrada y por sugerencia directa de los lectores.

1. PRIMERA PARTE:

LOS MISTERIOS DE ROMAN

Hace 15 días les mostré dos hermosos CPs del origamista Román Díaz y les indiqué, además, que entre sus líneas estaban ocultos grandes misterios. Para comenzar a entender los CPs me gustaría mostrarles uno de esos grandes misterios. Para ello, favor tocar la imagen que dice BASE.

___

CP__________________BASE

¡Eso es! Uno de los grandes misterios ocultos entre las líneas de los CPs es el modelo final del creador (en la entrada anterior, Introducción y Definición de CP, si tocan el otro CP se les revelará el otro modelo de Román).

A decir verdad, el modelo final está allí como una mariposa en el capullo. Y, ¿por qué lo expreso de esta manera? Porque es de gran importancia que entendamos muy bien los CPs y de este modo establezcamos los debidos límites de nuestro pasatiempo.

El CP usualmente nos lleva solo hasta lo que se denomina la BASE. En la terminología del Origami, la BASE de un modelo es una etapa en la secuencia de doblado en la que se obtiene una figura con la misma cantidad, distribución y tamaño de puntas o aletas principales que el modelo final. Algunas veces esa figura se parecerá al modelo final, pero por lo general no. Por lo tanto, para adentrarnos en este maravilloso pasatiempo que es la resolución de CPs, debemos quitarnos primero el deseo de obtener con ellos el modelo final del creador. Por supuesto, que a título personal y dependiendo de las capacidades de cada persona, muchos lograrán, mediante técnicas de origami, llegar al modelo final; pero eso ya estará fuera de los alcances de este blog.

En casos muy particulares, se logra encontrar creadores de origami bastante benévolos en cuyos CPs casi que se obtiene el modelo final, pero eso no es lo más común. Por lo tanto, como señalamos anteriormente lo más usual es que el CP nos lleve hasta la base, o hasta algún punto entre la base y el modelo final; pero definitivamente muy pocas veces hasta el modelo final y definitivamente nunca hasta antes de la base.

¡Me gusta pensar en la base!. La considero como un embrión del modelo final. En el CP-embrión está todo lo necesario o estructuralmente importante (ver definición de CP en la Introducción) para obtener la figura final, ¡pero le falta siempre algo más! Le falta crecer, desarrollarse, definirse y formar los detalles, para, de esta forma, al final, nacer. Los CPs son hermosos, con sus simetrías, sus vértices, de los cuales irradian múltiples rayos, formando como estrellas y el modelo final es grandioso, con su prestancia y representatividad; pero la base, a mi parecer es fea igual que un embrión. Muchas personas viendo el CP se sienten atraídas por resolverlo y al ver el modelo final desean obtenerlo, pero solo muy pocas, relativamente, sabiendo la verdad, persisten en desgastar su mente por el puro amor al "feo" embrión.

2. SEGUNDA PARTE:

LOS CPS MAS SENCILLOS Y SUS INCERTIDUMBRES

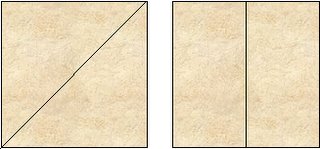
Las dos figuras de origami, con los CPs más sencillos que existen, sirven para representar montañas, volcanes, techos, libros, puertas, y miles de cosas más. Son de una gran antigüedad y sus orígenes se pierden en la nubosidad de la historia no documentada. Mostrarlos podría parecer trivial pero, como bien nos enseña el método inductivo, las cosas simples nos ayudarán a entender las complejas. En estos dos CPs están contenidos varios conceptos fundamentales que serán ampliamente utilizados en la resolución de CPs cada vez más complejos. Veamos los CPs trazados en un papel cuadrado:

(Fig.1) CP1: Bisectriz______ (Fig.2) CP2: Mediatriz

La línea del CP1 se denomina Bisectriz o Diagonal y corta el ángulo recto, de dos esquinas opuestas, exactamente en ángulos de 45°. Las figuras a ambos lados de la bisectriz son dos triángulos rectángulos isósceles, cada uno de ellos con un área que es la mitad del área del cuadrado original (¡Ojo los profesores de primaria, esto puede servir como método visual para la enseñanza de la geometría! Este blog contendrá muchos elementos que les pueden ser de utilidad.). Veámoslo con más detalle para que quede bien claro:

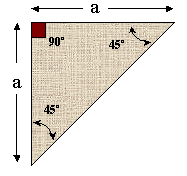
(Fig. 3) Cuadrado dividido__________(Fig.4) El triángulo separado

El triángulo es rectángulo por contener un ángulo de 90º y es isósceles puesto que tiene dos lados iguales.

El reconocimiento de figuras geométricas básicas y los conceptos matemáticos que las gobiernan será una parte fundamental en el proceso de resolución de CPS. Iremos poco a poco reconociéndolas una a una.

Por ahora solamente me gustaría mostrarles, para que los recuerden, los tipos de triángulos que existen:

(Fig. 5) Tipos de Triángulos

Volviendo a los CPs más sencillos, la figura 2 muestra la Mediatriz. La mediatriz corta el lado del cuadrado en dos, generando dos rectángulos, cada uno con un área que es la mitad del área del cuadrado original.

(Fig.6) Rectángulos

Ahora, tomemos una hoja de papel cuadrada y hagamos Origami (o sea, doblar papel en Japonés). ¡Doblemos el CP1! Entonces, la primera pregunta que nos hacemos es:

ACERTIJO NO.1

¿En qué dirección lo doblamos?

He querido resaltar esta pregunta debido a su importancia fundamental. La dirección del doblez es el primero de los grandes acertijos en la resolución de CPs. Para cada línea en un CP solo hay dos opciones de doblado hacia adelante o hacia atrás; pocas, ¡pero hay que DECIDIR!. Esta ambigüedad yo la llamo la PRIMERA INCERTIDUMBRE ESPACIAL: el CP no nos da la certeza de la dirección de doblado. Sin embargo, antes de analizar con detenimiento la primera incertidumbre espacial debemos establecer algunos elementos básicos más.

Aunque relativamente poco frecuente, algunos creadores de origami nos muestran el CP con el primero de los acertijos resuelto, pues nos indican la dirección de cada doblez. En este caso el CP se denomina CPMV que significa CP CON MONTAÑAS Y VALLES ASIGNADOS. Veamos con los CPs más sencillos a que nos referimos. Vamos a dibujar los dos CPMV de la diagonal. Para ello utilizamos la notación simbólica del origami:

(Fig.7) CPMV: en valle ____ (Fig.8) CPMV: en montaña

Entonces, las figuras tres y cuatro nos indican la dirección de los dobleces, la primera en valle y la segunda en montaña. Veamos ahora los diagramas de estos CPMV:

(Fig.9) Diagrama en valle_____ (Fig.10) Diagrama en montaña

Como pueden ver, para obtener los diagramas solo añadí las flechas. Ahora se leen así: para la figura 8 "doblar en la diagonal hacia adelante" y para la figura 9: "doblar en la diagonal hacia atrás" . ¡Hagámoslo con el papel! Si el papel es de dos colores, tendremos que considerar, si queremos el color seleccionado por dentro o por fuera. Pero, por ahora no consideraremos esta variable y pensaremos que el papel es del mismo color por ambos lados.

Bien, ¡ya lo hicimos!. Como pueden observar, para el caso de una sola línea es indiferente la dirección del doblez. ¡Trivial por ahora!

Todo lo que hemos escrito hasta ahora sirve también y de la misma manera para el CP de la mediatriz. Para ambos CPs, bisectriz o mediatriz, y para ambas líneas, valle o montaña, las figuras obtenidas se muestra en los siguientes diagramas:

(Fig.11) Triángulo rectángulo isósceles __(Fig.12) Rectángulo

Hemos obtenido estas dos figuras geométricas básicas y me gustaría con ellas indicarles un concepto más en la resolución de CPs. Si consideramos el papel como el plano, entonces estas figuras son realmente tridimensionales; sin embargo, lo común en origami es decir que son planas. Por lo tanto, me gusta llamarlas FIGURAS PLANAS MULTICAPAS, para diferenciarlas del plano; pero también, para diferenciarlas de las figuras de origami que si son propiamente tridimensionales, las cuales se llaman FIGURAS 3D.

Si los CPs son como los embriones de los modelos de origami; de seguro, la bisectriz o la mediatriz serían la columna vertebral. Son líneas "estructuralmente importantes" y son, a mi parecer, las primeras referencias en resolución de CPs. Sobre referencias ya nos dedicaremos bastante más adelante. Por ahora nos preguntaremos:

¿Qué sucederá con los CPs más sencillos si les incorporamos una nueva línea? ¿Qué variables y acertijos se nos propondrán como retos? Tengamos paciencia, que andando despacio se llega largo y seguro.

En este blog tus comentarios son extremadamente importantes; por favor escribirlos abajo. Si no tienes una cuenta ni un password no se preocupe, toque donde dice anónimo y allí puede escribir su mensaje.

Si deseas una copia en formato pdf de este documento solicítamelo a la dirección eric@internetelfaro.com que con mucho gusto te lo enviaré

Hasta dentro de 15 días.....